Hvad er sammenfaldende former?

Indhold

• Congruent cirkler
• parallelogrammer
• trekanter
• Sætninger for Congruent trekanter

For at to former skal være sammenhængende, skal hver have det samme antal sider, og deres vinkler skal også være de samme. De nemmeste måder at bestemme, om to figurer er sammenhængende, er at dreje den ene af figurerne, indtil den er indrettet sammen med den anden, eller blot stabel figurerne oven på hinanden for at se, om nogen ender stikker ud. Hvis du ikke er i stand til at bevæge figurerne fysisk, kan du bruge formler til at bestemme, om figurerne er kongruente.

Congruent cirkler

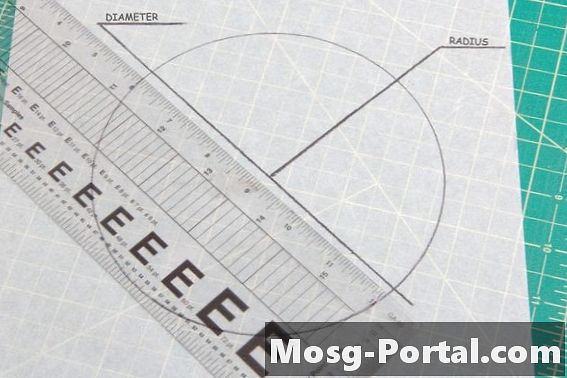
••• Ray Robert Green / Demand Media

Alle cirkler har den samme vinkel på 360 grader. Den eneste faktor til bestemmelse af sammenhængen mellem to cirkler er at sammenligne deres størrelse. Diameteren er en lige linje gennem centrum af cirklen fra kant til kant, mens radius for en cirkel er længden fra dens centrum til dens ydre kant. Måling af en af ​​disse på begge cirkler vil bevise, om de er kongruente.

parallelogrammer

••• Ray Robert Green / Demand Media

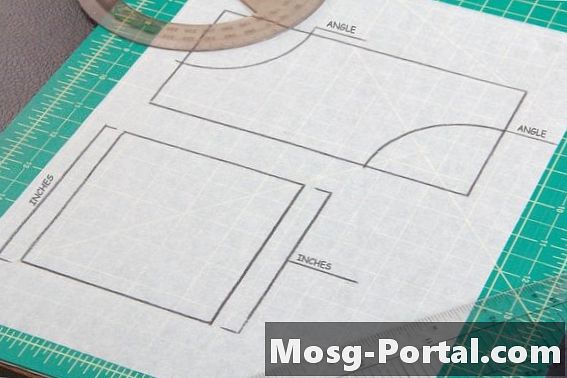
Et parallelogram har to par parallelle sider, såsom firkanter og rektangler. De modsatte sider eller vinkler på et parallelogram har samme mål, så det er nødvendigt at tage to vinkel- eller sidemålinger på et parallelogram, en fra hvert sidepar, for at sammenligne kongruens med en anden form.

trekanter

••• Ray Robert Green / Demand Media

For at finde sammenhæng mellem trekanter skal du bestemme størrelsen på hver vinkel eller side, da alle tre kan være forskellige. Der er tre postulater, der kan bruges til at identificere kongruente trekanter. SSS-postulatet er, når du måler alle tre sider til hver trekant. ASA-postulatet siger, at hvis to vinkler og deres forbindelsesside matcher den i den anden trekant, er de kongruente. SAS-postulatet gør det modsatte, og måler to sider og deres forbindelsesvinkel for at sammenligne med den anden trekant.

Sætninger for Congruent trekanter

••• Ray Robert Green / Demand Media

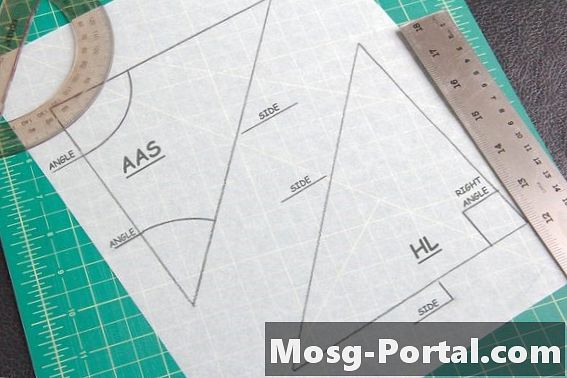
To sætninger er nyttige til at finde kongruente trekanter. AAS-sætningen siger, at hvis to vinkler og en side, der ikke forbinder de to, er lig med en anden trekant, så er de kongruente. Hypotenuse-Leg-sætningen gælder kun trekanter med en 90-graders eller "rigtig" vinkel. Dette er, når du måler hypotenusen - siden overfor 90 graders vinkel - og den ene af de andre sider af trekanten for at sammenligne med den anden form.