Indhold
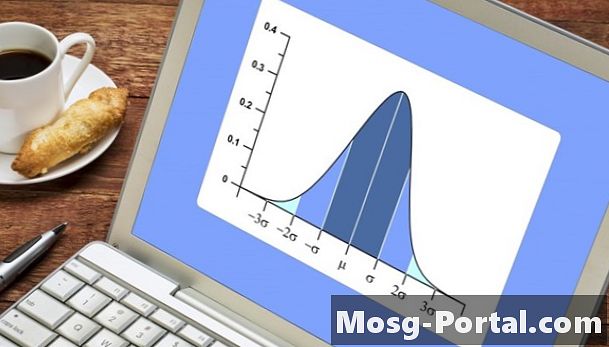
Efter at have taget en undersøgelse eller indsamlet numeriske data om en population, skal resultaterne analyseres for at hjælpe dig med at drage konklusioner. Du ønsker at vide parametre som det gennemsnitlige svar, hvor forskellige svarene var, og hvordan svarene er fordelt. En normal fordeling betyder, at dataene, når de er afbildet, skaber en klokkekurve, der er centreret om det gennemsnitlige respons og haler lige i både positive og negative retninger. Hvis dataene ikke er centreret om gennemsnittet, og den ene hale er længere end den anden, er fordelingen af data skæv. Du kan beregne mængden af skævhed i dataene ved hjælp af gennemsnittet, standardafvigelsen og antallet af datapunkter.
Beregn befolkningsskewness
Tilføj alle værdier i datasættet, og divider med antallet af datapunkter for at få gennemsnittet eller gennemsnittet. I dette eksempel antager vi et datasæt, der inkluderer svar fra en hel population: 2, 4, 5, 7, 8, 10, 11, 25, 26, 27, 36. Dette sæt har et gennemsnit på 14,6.
Beregn standardafvigelsen for datasættet ved at kvadrere forskellen mellem hvert datapunkt og middelværdien, tilføje alle disse resultater, derefter dividere med antallet af datapunkter og til sidst tage firkantsroden. Vores datasæt har en standardafvigelse på 11.1.
Find forskellen mellem hvert datapunkt og middelværdien, divider med standardafvigelsen, kub det nummer, og tilføj derefter alle disse tal sammen for hvert datapunkt. Dette svarer til 6,79.
Beregn befolkningens skævhed ved at dividere 6,79 med det samlede antal datapunkter. Befolkningsskævheden for dette eksempel er 0,617.
Beregn prøveskevhed
Beregn middel- og standardafvigelsen fra et datasæt, der kun er et stikprøve af hele befolkningen. Vi bruger det samme datasæt som det forrige eksempel med gennemsnit 14.6 og standardafvigelse 11.1, hvis vi antager, at disse tal kun er et stikprøve fra en større befolkning.
Find forskellen mellem hvert datapunkt og middelværdien, terning det antal, tilføj hvert resultat, og del derefter med terningen af standardafvigelsen. Dette svarer til 5,89.
Beregn prøveskævhed ved at multiplicere 5,89 med antallet af datapunkter divideret med antallet af datapunkter minus 1 og divideret igen med antallet af datapunkter minus 2. Eksempelskævhed for dette eksempel ville være 0,720.