Tangenten er en af de tre grundlæggende trigonometriske funktioner, hvor de to andre er sinus og kosinus. Disse funktioner er vigtige for studiet af trekanter og relaterer trekantens vinkler til dens sider. Den enkleste definition af tangenten bruger forholdet mellem siderne af en højre trekant, og moderne metoder udtrykker denne funktion som summen af en uendelig serie. Tangenter kan beregnes direkte, når længderne af siderne i den højre trekant er kendte, og de kan også afledes af andre trigonometriske funktioner.
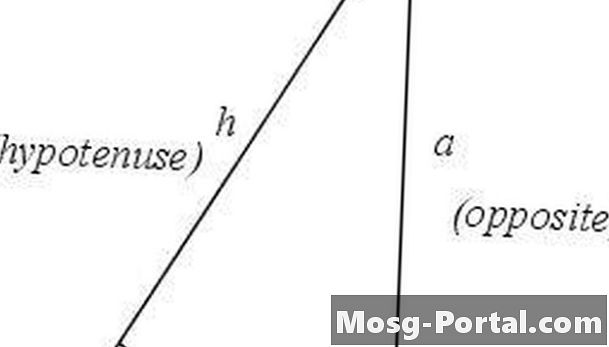
Identificer og mærk delene i en højre trekant. Den rigtige vinkel vil være i toppunktet C, og den modsatte side vil være hypotenusen h. Vinklen θ vil være i toppunktet A, og den resterende toppunkt vil være B. Den side, der støder op til vinklen θ, vil være side b, og den modsatte side af vinklen θ vil være siden a. De to sider af en trekant, der ikke er hypotenusen, er kendt som trekantenes ben.
Definer tangenten. Tangenten af en vinkel er defineret som forholdet mellem længden af siden modsat vinklen og længden af den side, der støder op til vinklen. For trekanten i trin 1, tan t = a / b.
Bestem tangenten for en simpel højre trekant. For eksempel er benene på en højre trekant af ensbenede enheder ens, så a / b = tan θ = 1. Vinklerne er også lige så θ = 45 grader. Derfor er brunfarve 45 grader = 1.
Afled tangenten fra de andre trigonometriske funktioner. Da sinus θ = a / h og cosinus θ = b / h, derefter sinus θ / cosinus θ = (a / h) / (b / h) = a / b = solbrun θ. Derfor tan θ = sinus θ / cosinus θ.
Beregn tangenten for enhver vinkel og ønsket nøjagtighed:
sin x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... cosinus x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Så tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)