Indhold
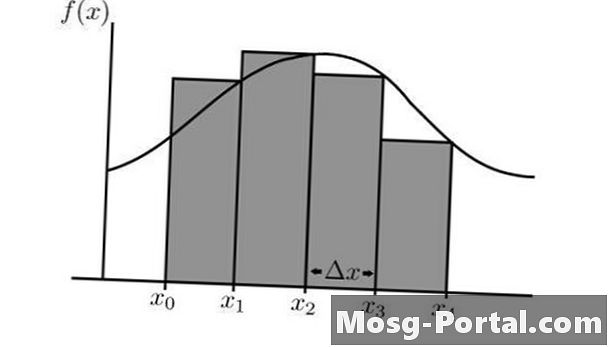
En Riemann-sum er en tilnærmelse af området under en matematisk kurve mellem to X-værdier. Dette område er tilnærmet ved hjælp af en række rektangler, der har en bredde på delta X, der er valgt, og en højde, der er afledt af den pågældende funktion, f (X). Jo mindre delta X er, jo mere præcis er tilnærmelsen. Højden kan tages fra værdien af f (X) enten til højre, midt eller venstre på rektanglet. Du kan lære, hvordan du beregner en venstre Riemann-sum.
Find værdien af f (X) ved den første X-værdi. Tag som et eksempel funktionen f (X) = X ^ 2, og vi nærmer os området under kurven mellem 1 og 3 med et delta X på 1; 1 er den første X-værdi i dette tilfælde, så f (1) = 1 ^ 2 = 1.
Multiplicer højden, som findes i det forrige trin, med delta X. Dette giver dig området for det første rektangel. For eksemplet er 1 x 1 = 1.
Føj delta X til den første X-værdi. Dette giver dig X-værdien i venstre side af det andet rektangel. For eksempel 1 + 1 = 2.
Gentag ovenstående trin for det andet rektangel. Fortsætter eksemplet, f (2) = 2 ^ 2 = 4; 4 x 1 = 4. Dette er området med det andet rektangel i eksemplet. Fortsæt på denne måde, indtil du har nået den endelige X-værdi. For eksemplet er der kun to rektangler, fordi 2 +1 = 3, hvilket er slutningen af det målte område.
Tilføj området med alle rektangler. Dette er Riemann-summen. Efterbehandling af eksemplet, 1 + 4 = 5.