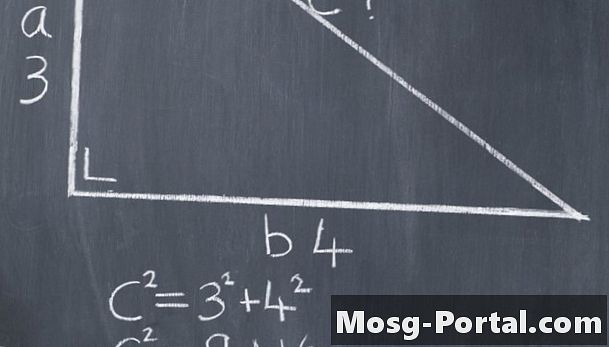
Indhold
En hypotenuse er den længste side af en højre trekant. Det er den side lige modsat fra den rigtige vinkel, og eleverne begynder først at lære dette udtryk i geometri i løbet af mellemskoleåret. Du kan finde længden, hvis enten de to andre sider af trekanten gives, eller et vinkelmål og en sidelængde.
Pythagoras sætning
I en højre trekant kaldes de to sider, der skaber en 90-graders vinkel, ben, og den lange side, der forbinder dem, kaldes hypotenusen. Du kan finde længden på hypotenusen fra to ben eller et ben og et vinkelmål. Pythagorean Theorem er en formel, der bruges til at finde længden på en af siderne i en højre trekant, når de får to sider. Formlen udtrykkes normalt som a ^ 2 + b ^ 2 = c ^ 2, hvor a og b er benene, og c er hypotenusen. Hvis du får a og b, kan du bruge dem og en vis algebra til at finde længden på hypotenusen. Uanset hvilken variabel der markeres hypotenusen, vil den side være c i Pythagorean Theorem formel.
Sæt den i
For at løse et problem med den rigtige trekant skal du altid finde den manglende side af en trekant ved hjælp af de to andre sider. For at finde hypotenusen skal du tilslutte værdierne for a og b. Se for eksempel på en trekant med sidelængder på 3 og 4. Hvis du tilslutter dem til formlen, 3 ^ 2 + 4 ^ 2 = c ^ 2, og forenkler, får du 9 + 16 = c ^ 2. Tilføjelse af 9 + 16 giver dig 25 = c ^ 2.
Løs ligningen
Når du har kvadratet benene og lagt dem sammen, skal du stadig få c af sig selv. For at få en variabel i sig selv i en ligning skal du anvende den kardinalregel for algebra: uanset hvad du gør på den ene side af ligningen, gør du også på den anden. I dette tilfælde har du brug for "c" i sig selv, da dette er længden på hypoteneuse. Ved at tage kvadratroden på 25 giver du kvadratroden af c ^ 2: c = 5.
Triple Triangles
Pythagorean Triples er rigtige trekanter, der har hele talværdier for hver side og kan bruges til at finde hypotenusen for nogle trekanter uden at foretage nogen beregninger. Der er mange forskellige tripler, men de mest almindelige er 3-4-5 og 5-12-13 trekanter. Disse sidelængder kan være faktorer i større trekanter, men de vil altid reduceres til en jævn tredobbelt. For eksempel, hvis du har benlængder på 10 og 24, kan du sætte dem i ligningen og tage kvadratroten af 10 ^ 2 + 24 ^ 2. Hvis du kender dine tredobbelte, vil du dog bemærke, at 10 og 24 er to gange 5 og 12, så hypotenusen skal være to gange 13 eller 26.