En ligesidet trekant er en trekant med alle tre sider af samme længde. Overfladearealet af en todimensionel polygon, såsom en trekant, er det samlede areal, der findes i polygonens sider. De tre vinkler i en ligesidet trekant er også af samme mål i den euklidiske geometri. Da det samlede mål for vinklerne i en euklidisk trekant er 180 grader, betyder det, at vinklerne på en lige sider trekant alle måler 60 grader. Arealet af en ligesidet trekant kan beregnes, når længden af den ene side er kendt.

Bestem arealet af en trekant, når basen og højden er kendt. Tag alle to identiske trekanter med basis s og højde h. Vi kan altid danne et parallelogram af basis s og højde h med disse to trekanter. Da arealet af et parallelogram er s x h, er arealet A i en trekant derfor ½ s x h.

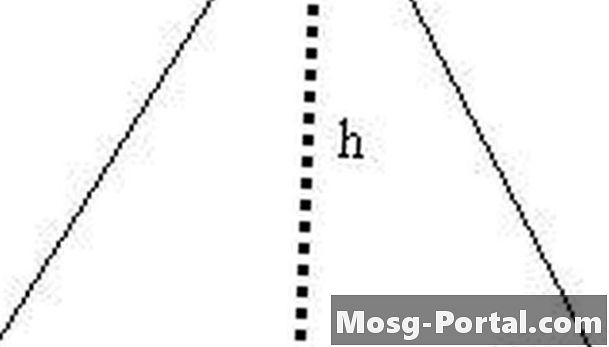
Form den ligesidede trekant i to højre trekanter med linjesegmentet h. Hypotenusen for en af disse højre trekanter er længde s, den ene af benene har længde h og den anden ben har længden s / 2.
Express h i form af s. Ved hjælp af den højre trekant, der er dannet i trin 2, ved vi, at s ^ 2 = (s / 2) ^ 2 + h ^ 2 med den Pythagoreiske formel. Derfor er h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, og vi har nu h = (3 ^ 1/2) s / 2.
Udskift værdien af h opnået i trin 3 i formlen for et trekantareal opnået i trin 1. Da A = ½ sxh og h = (3 ^ 1/2) s / 2, har vi nu A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Brug formlen til areal af en ligesidig trekant opnået i trin 4 til at finde arealet af en ligesidet trekant med sider af længde 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).