
Autokorrelation er en statistisk metode, der bruges til tidsserie-analyse. Formålet er at måle sammenhængen mellem to værdier i det samme datasæt på forskellige tidstrin. Selvom tidsdataene ikke bruges til beregnet autokorrelation, skal dine tidsforøgelser være ens for at få meningsfulde resultater. Autokorrelationskoefficienten tjener to formål. Det kan registrere ikke-tilfældighed i et datasæt. Hvis værdierne i datasættet ikke er tilfældige, kan autokorrelation hjælpe analytikeren med at vælge en passende tidsseriemodel.
Beregn gennemsnittet eller gennemsnittet for de data, du analyserer. Middelværdien er summen af alle dataværdier divideret med antallet af dataværdier (n).
Bestem en tidsforsinkelse (k) til din beregning. Forsinkelsesværdien er et heltal, der angiver, hvor mange tidstrin der adskiller en værdi fra en anden. For eksempel er forsinkelsen mellem (y1, t1) og (y6, t6) fem, fordi der er 6 - 1 = 5 tidstrin mellem de to værdier. Når du tester for tilfældighed, beregner du normalt kun en autokorrelationskoefficient ved hjælp af lag k = 1, selvom andre forsinkelsesværdier også fungerer. Når du bestemmer en passende tidsseriemodel, skal du beregne en række autokorrelationsværdier ved hjælp af en anden forsinkelsesværdi for hver.
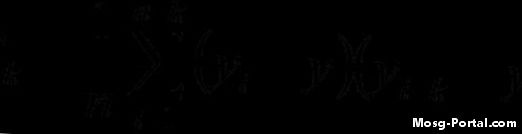
Beregn autocovariansfunktionen ved hjælp af den givne formel. For eksempel, beregner du den tredje iteration (i = 3) ved hjælp af en lag k = 7, så vil beregningen for den iteration se sådan ud: (y3 - y-bar) (y10 - y-bar) Iterere gennem alle værdier for "i", og tag derefter summen og divider den med antallet af værdier i datasættet.
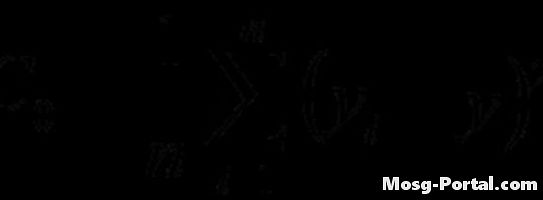
Beregn variansfunktionen ved hjælp af den givne formel. Beregningen ligner den for autocovariance-funktionen, men forsinkelse bruges ikke.

Del autokovariansfunktionen med variansfunktionen for at få autokorrelationskoefficienten. Du kan omgå dette trin ved at dele formlerne for de to funktioner som vist, men mange gange har du brug for autokovarians og varians til andre formål, så det er praktisk at beregne dem også individuelt.