Hvad er varmekapacitet?

Indhold

• Videnskaben om termodynamik
• Hvad er varmekapacitet?
• Varmekapacitet: enkle beregninger
• Hvad er forholdet mellem cp og cv γ?
• Luftens cp og cv

Varmekapacitet er et udtryk i fysik, der beskriver hvor meget varme der skal tilføjes et stof for at hæve dets temperatur med 1 grad Celsius. Dette er relateret til, men adskilt fra, specifik varme, som er den mængde varme, der er nødvendig for at hæve nøjagtigt 1 gram (eller en anden fast masseenhed) af et stof med 1 grad Celsius. At udlede en stoffer varmekapacitet C fra dens specifikke varme S handler om at multiplicere med mængden af ​​det stof, der er til stede, og sikre dig, at du bruger de samme masseenheder i hele problemet. Varmekapacitet er helt klart et indeks over en objekts evne til at modstå at blive opvarmet ved tilsætning af varmeenergi.

Materiale kan eksistere som et fast stof, en væske eller en gas. I tilfælde af gasser kan varmekapaciteten afhænge af både omgivelsestryk og omgivelsestemperatur. Forskere vil ofte vide, hvorvidt en gas er varmekapacitet ved konstant tryk, mens andre variabler, såsom temperatur, får lov til at ændre sig; dette er kendt som C_p. Tilsvarende kan det være nyttigt at bestemme en gasvarmekapacitet ved et konstant volumen eller C_v. Forholdet mellem C_p til C_v tilbyder vigtig information om de termodynamiske egenskaber ved en gas.

Videnskaben om termodynamik

Før du går i gang med en diskussion om varmekapacitet og specifik varme, er det nyttigt at først forstå det grundlæggende i varmeoverførsel i fysik og begrebet varme i almindelighed og sætte dig ind i nogle af de grundlæggende ligninger i disciplinen.

Termodynamik er den gren af ​​fysik, der beskæftiger sig med et systems arbejde og energi. Arbejde, energi og varme har alle de samme enheder i fysik på trods af at de har forskellige betydninger og anvendelser. SI (standard international) varmeenhed er joule. Arbejde defineres som kraft multipliceret med afstand, så med et øje på SI-enhederne for hver af disse mængder er en joule den samme ting som en Newton-meter. Andre enheder, du sandsynligvis vil støde på for varme, inkluderer kalorieindhold (cal), britiske termiske enheder (btu) og erg.(Bemærk, at de "kalorier", du ser på etiketter til madernæring, faktisk er kilokalorier, "kilo-" er det græske præfiks, der angiver "et tusind". Når du observerer, at f.eks. En 12 ounce dåse soda indeholder 120 " kalorier, "dette er faktisk lig med 120.000 kalorier i formelle fysiske termer.)

Gasser opfører sig forskelligt fra væsker og faste stoffer. Derfor har fysikere i verden af ​​aerodynamik og beslægtede discipliner, der naturligvis er meget optaget af opførslen af ​​luft og andre gasser i deres arbejde med højhastighedsmotorer og flyvemaskiner, særlige bekymringer omkring varmekapaciteten og andre kvantificerbare fysiske parametre relateret at betyder noget i denne tilstand. Et eksempel er enthalpi, som er et mål for den indre varme i et lukket system. Det er summen af ​​systemets energi plus produktet af dets tryk og volumen:

H = E + PV

Mere specifikt er ændringen i entalpi relateret til ændringen i gasvolumen ved forholdet:

∆H = E + P∆V

Det græske symbol ∆ eller delta betyder "ændring" eller "forskel" ved konvention i fysik og matematik. Derudover kan du kontrollere, at volumet af tryktider giver arbejdsenheder; trykket måles i newton / m², mens volumen kan udtrykkes i m³.

Tryk og volumen af ​​en gas er også relateret af ligningen:

P∆V = R∆T

hvor T er temperaturen, og R er en konstant, der har en anden værdi for hver gas.

Du behøver ikke at overføre disse ligninger til hukommelsen, men de vil blive revideret igen i diskussionen senere om C_p og C_v.

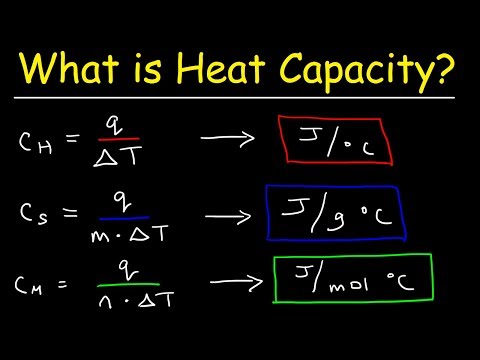
Hvad er varmekapacitet?

Som bemærket er varmekapacitet og specifik varme relaterede mængder. Den første opstår faktisk fra den anden. Specifik varme er en tilstandsvariabel, hvilket betyder, at den kun vedrører et stofs indre egenskaber og ikke til hvor meget af det der er til stede. Det udtrykkes derfor som varme pr. Masseenhed. Varmekapacitet afhænger på den anden side af, hvor meget af det pågældende stof gennemgår en varmeoverførsel, og det er ikke en tilstandsvariabel.

Alt stof har en temperatur der er forbundet med det. Dette er muligvis ikke den første ting, der kommer til at tænke på, når du bemærker et objekt ("Jeg spekulerer på, hvor varm denne bog er?"), Men undervejs har du måske lært, at forskere aldrig har formået at opnå en temperatur på absolut nul under alle omstændigheder, skønt de er kommet lidende tæt på. (Årsagen til at folk sigter mod at gøre sådan noget har at gøre med de ekstremt kolde materialers ekstremt høje ledningsevneegenskaber; tænk bare på værdien af ​​en fysisk elektrisk leder uden praktisk talt ingen modstand.) Temperatur er et mål for molekylers bevægelse . I faste materialer er stof arrangeret i et gitter eller gitter, og molekyler er ikke frie til at bevæge sig rundt. I en væske er molekyler mere fri til at bevæge sig, men de er stadig begrænset i vid udstrækning. I en gas kan molekyler bevæge sig meget frit. Husk under alle omstændigheder, at lav temperatur indebærer lille molekylær bevægelse.

Når du vil flytte et objekt, inklusive dig selv, fra et fysisk sted til et andet, skal du bruge energi - eller alternativt arbejde - for at gøre det. Du er nødt til at stå op og gå på tværs af et rum, eller du skal trykke på bilens gaspedal for at tvinge brændstof gennem dens motor og tvinge bilen til at bevæge sig. Tilsvarende på mikroniveau kræves et input af energi til et system for at få dets molekyler til at bevæge sig. Hvis dette input af energi er tilstrækkeligt til at forårsage en stigning i molekylær bevægelse, betyder det nødvendigvis, at stoffets temperatur også stiger på baggrund af ovenstående diskussion.

Forskellige almindelige stoffer har vidt forskellige værdier af specifik varme. Blandt metaller kontrolleres for eksempel guld ved 0,129 J / g ° C, hvilket betyder, at 0,139 joule varme er tilstrækkelig til at hæve temperaturen på 1 gram guld med 1 grad Celsius. Husk, at denne værdi ikke ændres baseret på mængden af ​​guld, der er til stede, fordi massen allerede er redegjort for i nævneren for de specifikke varmeenheder. Dette er ikke tilfældet med varmekapacitet, som du snart vil opdage.

Varmekapacitet: enkle beregninger

Det overrasker mange studerende i introduktionsfysik, at den specifikke vandvarme, 4.179, er betydeligt højere end hos almindelige metaller. (I denne artikel er alle værdier for specifik varme angivet i J / g ° C.) Isens varmekapacitet, 2,03, er også mindre end halvdelen af ​​vandets, selvom begge består af H₂O. Dette viser, at tilstanden af ​​en forbindelse og ikke kun dens molekylære sammensætning påvirker værdien af ​​dens specifikke varme.

Under alle omstændigheder skal du sige, at du bliver bedt om at bestemme, hvor meget varme der kræves for at hæve temperaturen på 150 g jern (som har en bestemt varme, eller S, på 0,450) med 5 C. Hvordan ville du gøre noget ved dette?

Beregningen er meget enkel; multiplicer den specifikke varme S med mængden af ​​materiale og ændringen i temperatur. Da S = 0,450 J / g ° C, er den mængde varme, der skal tilføjes i J, (0,450) (g) (∆T) = (0,450) (150) (5) = 337,5 J. En anden måde at udtrykke det vil sige, at varmekapaciteten til 150 g jern er 67,5 J, hvilket ikke er andet end den specifikke varme S ganget med massen af ​​det tilstedeværende stof. Selvom varmekapaciteten i flydende vand er konstant ved en given temperatur, ville det naturligvis tage meget mere varme at varme en af ​​de store søer med en tiendedel grad end det ville tage at opvarme en pint vand med 1 grad eller 10 eller endda 50.

Hvad er forholdet mellem cp og cv γ?

I et tidligere afsnit blev du introduceret til ideen om betingede varmekapaciteter for gasser - det vil sige varmekapacitetsværdier, der gælder for et givet stof under forhold, hvor enten temperaturen (T) eller trykket (P) holdes konstant gennem hele problemet. Du fik også de grundlæggende ligninger ∆H = E + P∆V og P∆V = R∆T.

Fra de sidstnævnte to ligninger kan du se, at en anden måde at udtrykke ændring i entalpi, ∆H, er:

E + R∆T

Selvom der ikke findes nogen afledning her, er en måde at udtrykke den første lov om termodynamik, der gælder for lukkede systemer, og som du muligvis har hørt på en fælles måde sagt som "Energi hverken er skabt eller ødelagt," at være:

∆E = C_vAT

På almindeligt sprog betyder det, at når en bestemt mængde energi tilføjes et system, der inkluderer en gas, og volumen af ​​denne gas ikke får lov til at ændre sig (angivet med underskriptet V i C_v), skal temperaturen stige i direkte forhold til værdien af ​​gasens varmekapacitet.

Et andet forhold findes mellem disse variabler, der muliggør afledning af varmekapacitet ved konstant tryk, C_p, snarere end konstant volumen. Dette forhold er en anden måde at beskrive entalpi på:

∆H = C_pAT

Hvis du er adroit på algebra, kan du nå frem til et kritisk forhold mellem C_v og C_p:

C_p = C_v + R

Det vil sige, varmekapaciteten af ​​en gas ved konstant tryk er større end dens varmekapacitet ved konstant volumen med en eller anden konstant R, der er relateret til de specifikke egenskaber for den gas, der undersøges. Dette giver intuitiv mening; hvis du forestiller dig, at en gas får lov til at ekspandere som svar på stigende internt tryk, kan du sandsynligvis opfatte, at den bliver nødt til at varme op mindre som svar på en given tilsætning af energi, end hvis den var begrænset til det samme rum.

Endelig kan du bruge al denne information til at definere en anden substansspecifik variabel, γ, som er forholdet mellem C_p til C_veller C_p/ C_v. Du kan se fra den forrige ligning, at dette forhold stiger for gasser med højere værdier af R.

Luftens cp og cv

C_p og C_v luft er begge vigtige i studiet af væskedynamik, fordi luft (bestående af en blanding af for det meste nitrogen og ilt) er den mest almindelige gas, som mennesker oplever. Begge C_p og C_v er temperaturafhængige og ikke nøjagtigt i samme omfang; som det sker, C_v stiger lidt hurtigere med stigende temperatur. Dette betyder, at den "konstante" y faktisk ikke er konstant, men den er overraskende tæt på tværs af en række sandsynlige temperaturer. For eksempel ved 300 grader Kelvin eller K (lig med 27 C) er værdien af ​​y 1.400; ved en temperatur på 400 K, hvilket er 127 ° C og betydeligt over vandets kogepunkt, er værdien af ​​y 1,395.