Indhold
Sines lov og kosines lov er trigonometriske formler, der vedrører målingerne af vinklerne i en trekant til længderne af dens sider. De er afledt af egenskaben, at større vinkler i trekanter har forholdsvis større modsatte sider. Brug sines-loven eller kosinus-loven til at beregne længderne på siderne af en trekant og firkantet (en firkantet er i det væsentlige to tilstødende trekanter), hvis du kender målene for den ene side, en vinkel og en yderligere side eller vinkel.
Beregn trekantens sidelængder
Find trekanterne. Giverne er længder på sider og målinger af vinkler, der allerede er kendt.Du kan ikke finde målet på trekantens sidelængder, medmindre du kender målene for en vinkel, en side og enten en anden side eller en anden vinkel.
Brug giverne til at bestemme, om trekanten er en ASA-, AAS-, SAS- eller ASS-trekant. En ASA trekant har to vinkler som giver såvel som den side, der forbinder de to vinkler. En AAS trekant har to vinkler og en anden side som giver. En SAS trekant har to sider som giver såvel som vinklen dannet af de to sider. En ASS-trekant har to sider og en anden vinkel som giverne.
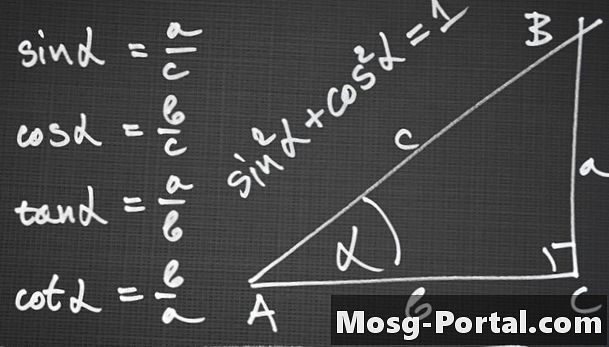
Brug sines lovgivningen til at oprette en ligning, der vedrører sidelængderne, hvis det er en ASA-, AAS- eller ASS-trekant. Sines loven siger, at forholdet mellem sines af en trekants vinkler og deres modsatte sider er lige: sin A / a = sin B / b = sin C / c, hvor a, b og c er de modsatte sidelængder af vinkler A, B og C.
For eksempel, hvis du ved, at to vinkler er 40 grader og 60 grader, og den side, der sammenføjede dem med var 3 enheder lang, ville du oprette ligningen sin 80/3 = sin 40 / b = sin 60 / c (du kender den modsatte vinkel den side, der er 3 enheder lang, er 80 grader, fordi summen af trekantens vinkler er 180 grader).
Brug kosinusloven til at oprette en ligning, der vedrører sidelængderne, hvis det er en SAS trekant. Kosinusloven siger, at c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C. Med andre ord er kvadratet på længden af side c lig med kvadraterne for de to andre sidelængder minus produktet af disse to sider og kosinus i vinklen overfor den ukendte side. For eksempel, hvis de to sider var 3 enheder og 4 enheder, og vinklen var 60 grader, ville du skrive ligningen c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60.
Løs for variablerne i ligningerne for at finde de ukendte trekantlængder. Opløsning for b i ligningen sin 80/3 = sin 40 / b giver værdien b = 3 sin 40 / sin 80, så b er cirka 2. Opløsning for c i ligningen sin 80/3 = sin 60 / c giver værdi c = 3 sin 60 / sin 80, så c er ca. 2,6. Tilsvarende giver opløsning for c i ligningen c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 værdien c ^ 2 = 25 - 6 eller c ^ 2 = 19, så c er ca. 4,4.
Beregn firkantede sidelængder
Tegn en diagonal gennem det firkantede (vælg den diagonale, der ikke inkluderer nogen givne vinkelmålinger; for eksempel hvis vinkel A er en given i firkantede ABCD, tegnes diagonalforbindelsen B og D).
Brug giverne til at opsætte en ASA-, SAS-, AAS- eller ASS-trekant. Husk, at summen af vinklerne på et firsidet tværs er 360 grader, så du kan finde et mål på den fjerde vinkel, hvis du kender de andre tre.
Brug sines lovgivningen til at løse længderne på siderne af det firkantede, hvis du opretter en ASA, AAS eller ASS trekant. Brug kosinusloven til at løse sidelængderne, hvis du opretter en SAS trekant.