En ellipse kan defineres i plangeometri som sæt af punkter, således at summen af deres afstande til to punkter (foci) er konstant. Det resulterende tal kan også beskrives ikke-matematisk som en oval eller "flad cirkel". Ellipser har en række anvendelser inden for fysik og er især nyttige til at beskrive planetariske kredsløb. Excentricitet er en af egenskaberne ved og ellipse og er et mål for, hvor cirkulær ellipsen er.
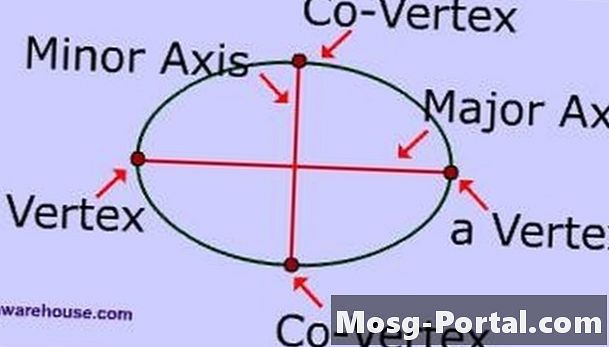
Undersøg dele af en ellips. Hovedaksen er det længste linjesegment, der skærer midten af ellipsen og har sine endepunkter på ellipsen. Den mindre akse er det korteste linjesegment, der skærer midten af ellipsen og har sine endepunkter på ellipsen. Den største halvakse er halvdelen af hovedaksen, og den mindre halvakse er halvdelen af mindre aksen.
Undersøg formlen for en ellipse. Der er mange forskellige måder at beskrive en ellipse matematisk på, men den mest nyttige til beregning af dens eksentricitet er for en ellipse er følgende: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konstanterne a og b er specifikke for en bestemt ellipse, og variablerne er x- og y-koordinaterne for punkter, der ligger på ellipsen. Denne ligning beskriver en ellipse med dens centrum ved oprindelsen og større og mindre akser, der ligger på x- og y-oprindelsen.
Identificer længden af halvakslerne. I ligningen x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, er længdene af halvakslerne angivet med a og b. Den større værdi repræsenterer den vigtigste halvakse, og den mindre værdi repræsenterer den mindre halvakse.
Beregn placeringerne for fociene. Fociene er placeret på hovedaksen, en på hver side af midten. Da ellipsens akser ligger på oprindelseslinjerne, vil en koordinat være 0 for begge fokuser. Den anden koordinat for vil være (a ^ 2 - b ^ 2) ^ (1/2) for den ene foci og - (a ^ 2 - b ^ 2) ^ (1/2) for den anden fokus, hvor a> b.
Beregn ellipsens excentricitet som forholdet mellem afstanden for et fokus fra centrum til længden af den halv-store akse. Eksentriciteten e er derfor (a ^ 2 - b ^ 2) ^ (1/2) / a. Bemærk, at 0 <= e <1 for alle ellipser. En excentricitet på 0 betyder ellipsen er en cirkel, og en lang, tynd ellipse har en excentricitet, der nærmer sig 1.